Улитка Паскаля

Обзорная статья: Окружность

Семь форм улиток Паскаля как конхоиды чёрной окружности с полюсом (0, 0): $r(\varphi )=2a\cos \varphi +l.$ Из них красная — с параболической точкой распрямления, зелёная — кардиоида, синяя — трисектриса

Страница книги Дюрера 1525 года с линией паука (Spinnenlinie)

Ули́тка Паска́ля (англ. limacon of Pascal, от лат. limax — улитка) ― конхоида окружности с полюсом на этой окружности.

Обычно представляется следующим уравнением конхоиды окружности в полярной системе координат:

$r(\varphi )=2a\cos \varphi +l,$

где $a$ — радиус базовой окружности конхоиды; $l$ — приращение радиус-вектора окружности, проведённого из полюса конхоиды на окружности.

Относится к плоским алгебраически кривым 4-го порядка.

Улитка Паскаля — это кривая, обладающая следующими простыми свойствами:

• ограниченная и замкнутая;
• связная только для кардиоиды и улитки с петлёй, остальные кривые имеют изолированную точку;
• имеет одну особую точку — двойную: точку самопересечения, касп или изолированную в зависимости от параметров;
• имеет одну ось симметрии.

Названа по имени французского учёного Этьена Паскаля (отца Блеза Паскаля), рассмотревшего её в первой половине XVII века. Улитка Паскаля изучалась Альбрехтом Дюрером в 1525 году под названием арахна (линия паука) (англ. Arachne; нем. Spinnenlinie; фр. arachnée), Этьеном Паскалем в 1630 году и Жилем Робервалем, который и назвал кривую «улиткой Паскаля» в 1650 году.

Определения улитки Паскаля

Самые распространённые определение и уравнение

Ули́тка Паска́ля (англ. limacon of Pascal; Pascal’s snail; snail curve) ― конхоида окружности с полюсом на этой окружности, обычно задаваемая следующим уравнением в полярной системе координат:

$r(\varphi )=2a\cos \varphi +l,$

где $a$ — радиус базовой окружности $\,r(\varphi )=2a\cos \varphi \,$ конхоиды; $l$ — приращение радиус-вектора окружности, проведённого из полюса конхоиды.

Базовая окружность $\,r(\varphi )=2a\cos \varphi \,$ улитки Паскаля называется также её директрисой, а приращение радиус-вектора $l$ — её модулем.

Улитка Паскаля — это кривая, обладающая следующими основными свойствами:

• ограниченная и замкнутая;
• связная только для кардиоиды и улитки с петлёй, остальные кривые имеют изолированную точку;
• имеет одну особую точку — двойную: точку самопересечения, касп или изолированную в зависимости от параметров;
• имеет одну ось симметрии.

Обычное уравнение улитки Паскаля в полярой системе координат

$r=2a\cos \varphi +l,$

может быть записано по-другому:

• в сокращённой форме:

$r=d\cos \varphi +l,$

где $d$ — диаметр базовой окружности конхоиды;

• в размерно-безразмерной форме:

$r=l(e\cos \varphi +1),$

где $le=2a$ — диаметр базовой окружности конхоиды; $e={\frac {2a}{l}}$ — безразмерный параметр;

• в безразмерной форме:

$\rho =2\cos \varphi +\epsilon ,$

где $\rho ={\frac {r}{a}},\,$ $\epsilon ={\frac {l}{a}}$ — безразмерные параметры.

Все уравнения, рассмотренные выше, имеют горизонтальную ось симметрии (совпадающую с оью абсцисс) и как полюс коноиды, так и особые точки, расположенные слева. Но особые точки можно расположить на графике и справа, записав уравнение улитки Паскаля в следующей форме:

$r=-2a\cos \varphi +l,$

У всех уравнений, рассмотренные выше, ось симметрии совпадает с осью абсцисс. У следующих уравнений ось симметрии улитки Паскаля совпадает с осью ординат:

• полюс коноиды и особые точки расположены вверху:

$r=-2a\sin \varphi +l;$

• полюс коноиды и особые точки расположены внизу:

$r=2a\sin \varphi +l.$

Вывод уравнения и геометрическое построение

Геометрическое построение красной точки улитки Паскаля (трисектрисы, $l=a$)

Детализируем определение улитки Паскаля, расшифровав понятие конхоиды:

ули́тка Паска́ля — геометрическое место концов радиус-векторов, проведённых из фиксированной точки на окружности радиуса $a$ ко всем точкам окружности, причём эти радиус-векторы увеличены (одна ветвь) или уменьшены (другая ветвь) на постоянную величину $l$.

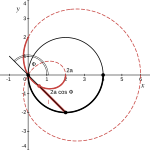
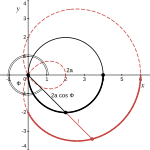
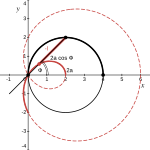
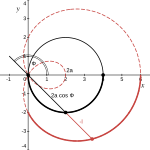
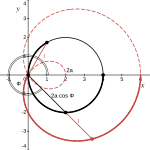
Получим уравнение улитки Паскаля в полярной системе координат. Для этого (см. рисунок справа):

• поместим полюс конхоиды, расположенный на базовой окружности, в начало полярной системы координат;
• расположим диаметр базовой окружности на полярной оси справа от начала координат;
• положим, что $l<2a$ (на рисунке справа $l=a$),

тогда получаем, что (см. рисунок справа):

• радиус-вектор из определения равен

$r(\varphi )=2a\cos \varphi ;$

• увеличенный на $l$ радиус-вектор из определения равен

$r(\varphi )=2a\cos \varphi +l,$

и последнее уравнение есть уравнение одной ветви улитки Паскаля.

Очевидно, что уравнение другой ветви улитки Паскаля будет

$r(\varphi )=2a\cos \varphi -l.$

Поскольку

$r(\varphi )=2a\cos \varphi +l=2a\cos(\pi +\varphi )-l,$

то ветви улитки Паскаля как конхоиды окружности совпадают, что показано на рисунках ниже, и в качестве уравнения улитки Паскаля можно взять уравнение одной из ветвей, обычно берут первое:

$r(\varphi )=2a\cos \varphi +l.$

Для первой ветви при повороте радиус-вектора от $0^{\circ }$ до $180^{\circ }$ конец увеличенного радиус-вектора описывает верхнюю половину большой дуги улитки Паскаля и нижнюю половину петли, если она есть. При дальнейшем повороте радиус-вектора получаются остальные части первой ветви улитки Паскаля. Даже если радиус-вектор первой ветви отрицательный, то его увеличение откладывается от его конца всё равно в положительном направлении. Картина аналогична для второй ветви, когда уменьшение радиус-вектора всегда откладывается в отрицательном направлении. На рисунках ниже показаны три серии построения:

• обеих ветвей улитки Паскаля, имеющей петлю (трисектрисы), отдельно в четырёх квадрантах плоскости;
• улитки Паскаля, имеющей петлю (трисектрисы), для случая, когда её радиус-вектор всегда неотрицателен, то есть при $r(\varphi )=2a\cos \varphi +l\geqslant 0;$

Если улитка Паскаля не имеет петли, то её первая ветвь всегда имеет неотрицательный радиус-вектор, а вторая ветвь — неположительный.

Конхоидное преобразование улитки Паскаля (не окружности)

$r(\varphi )=2a\cos \varphi +l$

с полюсом этой же улитки и с модулем $l'$ есть снова улитка Паскаля

$r(\varphi )=2a\cos \varphi +l\pm l'$,

но в этом случае ветви всегда будут разные, причём если $l'=l$, то вторая ветвь будет окружностью.

• Первая ветвь улитки Паскаля (трисектрисы) для квадрантов плоскости
• 
  $r(\varphi )=2a\cos \varphi +l,$ $0^{\circ }\leqslant \varphi \leqslant 90^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi +l,$ $90^{\circ }\leqslant \varphi \leqslant 180^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi +l,$ $180^{\circ }\leqslant \varphi \leqslant 270^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi +l,$ $270^{\circ }\leqslant \varphi \leqslant 360^{\circ }$

• Вторая ветвь улитки Паскаля (трисектрисы) для квадрантов плоскости
• 
  $r(\varphi )=2a\cos \varphi -l,$ $0^{\circ }\leqslant \varphi \leqslant 90^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi -l,$ $90^{\circ }\leqslant \varphi \leqslant 180^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi -l,$ $180^{\circ }\leqslant \varphi \leqslant 270^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi -l,$ $270^{\circ }\leqslant \varphi \leqslant 360^{\circ }$

• Обе ветви улитки Паскаля (трисектрисы) для квадрантов плоскости при неотрицательном радиус-векторе
• 
  $r(\varphi )=2a\cos \varphi +l,$ $r(\varphi )\geqslant 0,$ $0^{\circ }\leqslant \varphi \leqslant 180^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi +l,$ $r(\varphi )\geqslant 0,$ $180^{\circ }\leqslant \varphi \leqslant 360^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi -l,$ $r(\varphi )\geqslant 0,$ $0^{\circ }\leqslant \varphi \leqslant 180^{\circ }$
• 
  $r(\varphi )=2a\cos \varphi -l,$ $r(\varphi )\geqslant 0,$ $180^{\circ }\leqslant \varphi \leqslant 360^{\circ }$

Виды улиток Паскаля

Примечательные точки улитки Паскаля

Существуют три вида улиток Паскаля: гиперболические, параболические (кардиоиды) и эллиптические. Будем использовать уравнение улитки Паскаля

$r(\varphi )=2a\cos \varphi +l.$

Гиперболические улитки Паскаля $r(\varphi )=2a\cos \varphi +l,\,$ $l<2a$ с примечательными точками и касателными в точках самопересечения

Две касательные прямые всех улиток Паскаля в особой точке — полюсе конхоиды, он же начало координат $r=0,$ — имеют следующее уравнение:

$4a^{2}\cos ^{2}\varphi -l^{2}=0,$

поэтому (см. рисунки справа):

• если $l<2a,$ то касательные действительные, и особая точка — точка самопересечения параболической улитки Паскаля;
• если $l=2a,$ то касательные совпадают с осью абсцисс, и особая точка — касп кардиоиды;
• если $l>2a,$ то касательные мнимые, и особая точка — изолированная эллиптической улитки Паскаля.

Вершины всех видов улиток Паскаля, если они есть, удовлетворяют следующему уравнению, полученному приравниванием нулю производной

$\kappa '(\varphi )={\frac {12a^{2}l\sin \varphi (l\cos \varphi +2a)}{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{5}}}$

кривизны

$\kappa (\varphi )={\frac {6al\cos \varphi +8a^{2}+l^{2}}{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{3}}},$

то есть это необходимое условие быть вершиной (но не достаточное):

$\sin \varphi (l\cos \varphi +2a)=0.$

Вывод уравнения кривизны и её производной

Перейдём от уравнения в полярных координатах

$r(\varphi )=2a\cos \varphi +l.$

к параметрическому уравнению, взяв в качестве уравнений проекции улитки Паскаля на декартовы координаты:

$x=(2a\cos \varphi +l)\cos \varphi ,$

$y=(2a\cos \varphi +l)\sin \varphi .$

Вычислим производные этих уравнений:

$x'=-(4a\cos \varphi +l)\sin \varphi ,$

$y'=4a\cos ^{2}\varphi +l\cos \varphi -2a,$

$x''=-8a\cos ^{2}\varphi +l\cos \varphi -4a,$

$y''=-(8a\cos \varphi +l)\sin \varphi$

и получим уравнение кривизны

$\kappa (\varphi )={\frac {x'y''-x''y'}{({\sqrt {x'^{2}+y'^{2}}})^{3}}},$

$x'y''-x''y'=32a^{2}\cos ^{2}\varphi +12al\cos \varphi +l^{2}-{}$

${}-32a^{2}\cos ^{4}\varphi -12al\cos ^{3}\varphi -l^{2}\cos ^{2}\varphi +{}$

${}+32a^{2}\cos ^{4}\varphi +8al\cos ^{3}\varphi -16a^{2}\cos ^{2}\varphi +{}$

${}+4al\cos ^{3}\varphi +l^{2}\cos ^{2}\varphi -2al\cos \varphi -{}$

${}-16a^{2}\cos ^{2}\varphi -4al\cos \varphi +8a^{2}=$

$=6al\cos \varphi +l^{2}+8a^{2},$

$x'^{2}+y'^{2}=16a^{2}\cos ^{2}\varphi +8al\cos \varphi +l^{2}-{}$

${}-16a^{2}\cos ^{4}\varphi -8al\cos ^{3}\varphi -l^{2}\cos ^{2}\varphi +{}$

${}+16a^{2}\cos ^{4}\varphi +8al\cos ^{3}\varphi +l^{2}\cos ^{2}\varphi -{}$

${}-16a^{2}\cos ^{2}\varphi -4al\cos \varphi +4a^{2}=$

$=4al\cos \varphi +l^{2}+4a^{2},$

$\kappa (\varphi )={\frac {6al\cos \varphi +8a^{2}+l^{2}}{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{3}}}.$

Осталось найти производную кривизны

$\kappa '(\varphi )=\left({\frac {6al\cos \varphi +8a^{2}+l^{2}}{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{3}}}\right)'=$

$={\frac {-6al\sin \varphi }{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{3}}}+{}$

${}+{\frac {3(6al\cos \varphi +8a^{2}+l^{2})(4al\sin \varphi )}{2({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{5}}}=$

$={\frac {-48a^{2}l^{2}\cos \varphi \sin \varphi -48a^{3}l\sin \varphi -12al^{3}\sin \varphi }{2({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{5}}}+{}$

${}+{\frac {72a^{2}l^{2}\cos \varphi \sin \varphi +96a^{3}l\sin \varphi +12al^{3}\sin \varphi }{2({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{5}}}=$

$={\frac {12a^{2}l^{2}\cos \varphi \sin \varphi +24a^{3}l\sin \varphi }{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{5}}}=$

$={\frac {12a^{2}l\sin \varphi (l\cos \varphi +2a)}{({\sqrt {4al\cos \varphi +4a^{2}+l^{2}}})^{5}}}.$

Эллиптические улитки Паскаля $r(\varphi )=2a\cos \varphi +l,\,$ $l>2a$ с примечательными точками

Последнее уравнение есть совокупность уравнений

$\left[{\begin{array}{rcl}\sin \varphi =0,\\l\cos \varphi +2a=0,\end{array}}\right.$

откуда вершины, если они есть, имеют координаты (см. рисунки справа)

$\left[{\begin{array}{lcl}\sin \varphi =0,\quad r=l\pm 2a,\\\displaystyle \cos \varphi =-{\frac {2a}{l}},\quad r=l-{\frac {4a^{2}}{l}}\end{array}}\right.$

и лежат на прямой и циссоиде Диокла (см. рисунок справа)

$\left[{\begin{array}{lcl}\sin \varphi =0,\\\displaystyle r=2a\left(\cos \varphi -{\frac {1}{\cos \varphi }}\right)=-{\frac {2a\sin ^{2}\varphi }{\cos \varphi }}.\end{array}}\right.$

Грушевидная квартика, составленная из точек перегиба эллиптических улиток Паскаля $r(\varphi )=2a\cos \varphi +l,\,$ $l>2a$

Точки перегиба эллиптических улиток Паскаля, если они есть, удовлетворяют следующему уравнению, полученному приравниванием нулю кривизны, то есть это необходимое условие быть точкой перегиба (но не достаточное):

$6al\cos \varphi +l^{2}+8a^{2}=0,$

откуда точки перегиба, если они есть, имеют координаты (см. рисунки справа)

$\cos \varphi =-{\frac {l^{2}+8a^{2}}{6al}},$

$r=l-{\frac {l^{2}+8a^{2}}{3l}}={\frac {2l^{2}-8a^{2}}{3l}}.$

и лежат на обобщённой грушевидной квартике (см. рисунок справа)

$r^{2}+2ar\cos \varphi -8a^{2}\cos ^{2}\varphi +8a^{2}=0,$

или

$r^{2}+2ar\cos \varphi +8a^{2}\sin ^{2}\varphi =0,$

или

$(r+a\cos \varphi )^{2}+a^{2}(8\sin ^{2}\varphi -\cos ^{2}\varphi )=0.$

Гиперболическая улитка Паскаля

Трисектриса $r(\varphi )=a(2\cos \varphi +1),\,$ $a=2$ с точкой самопересечения и двумя вершинами

Гиперболическая улитка (англ. hyperbolic limacon) — улитка Паскаля, у которой параметры отвечают следующему неравенству:

$l<2a.$

Синоним:

• улитка с петлёй (англ. limacon with a loop; crunodal limacon).

Частные случаи:

• улитка Паскаля вырождается в окружность радиуса $a$ при

$l=0,$

то есть уравнение окружности

$r(\varphi )=2a\cos \varphi ;$

• улитка Паскаля есть трисектриса (англ. trisectrix; англ. limaçon trisectrix) при

$l=a,$

то есть её уравнение

$r(\varphi )=a(2\cos \varphi +1).$

Перечислим примечательные точки трисектрисы как типичного представителя улитки с петлёй (см. рисунок справа):

• трисектриса имеет точку самопересечения в начале координат $r=0;$
• радиальные координаты кандидатов в точки перегиба

$\cos \varphi =-{\frac {3}{2}}<-1,\,$ $r={\frac {2l^{2}-8a^{2}}{3l}}=-2a,$

поэтому точек перегиба нет;

• из вершин попадают на кардиоиду и не попадают на точку самопересечения только две точки

$\varphi =0,\,r=3a$ и $\varphi =\pi ,\,r=-a.$

Параболическая улитка Паскаля

Кардиоида $r(\varphi )=2a(\cos \varphi +1),\,$ $a=2$ с каспом и вершиной

Основная статья: Кардиоида

Параболическая улитка (англ. parabolic limacon) — улитка Паскаля, у которой параметры отвечают следующему равенству:

$l=2a,$

то есть её уравнение

$r(\varphi )=2a(\cos \varphi +1).$

Синонимы:

• улитка с каспом (англ. cuspidal limacon),
• кардиоида (англ. cardioid),

Перечислим примечательные точки кардиоиды (см. рисунок справа):

• кардиоида имеет касп в начале координат $r=0;$
• радиальная координата кандидата в точки перегиба

$r={\frac {2l^{2}-8a^{2}}{3l}}=0,$

поэтому точек перегиба нет, точка $r=0$ — это касп;

• из вершин попадает на кардиоиду и не попадает на касп только точка

$\varphi =0,\quad r=4a.$

Эллиптическая улитка Паскаля

Эллиптическая улитка (англ. elliptic limacon) — улитка Паскаля, у которой параметры отвечают следующему неравенству:

$l>2a.$

Синонимы:

• улитка с изолированной точкой (англ. limacon with an isolated point; acnodal limacon);
• обычная улитка (англ. ordinary limaçon).

Частные случаи:

• улитка в форме фасолины (англ. limacon with the shape of a bean) при

$2a<l<4a;$

• улитка с параболической точкой распрямления (англ. limacon with a meplat) при

$l=4a;$

• выпуклая улитка (англ. convex limacon) при

$4a<l<\infty ;$

• улитка Паскаля вырождается в окружность бесконечного радиуса при

$l\rightarrow \infty .$

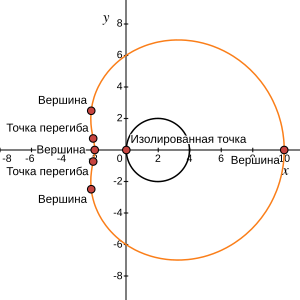
Перечислим примечательные точки представителя улитки в форме фасолины с $l=4a$ (см. рисунок ниже):

• улитка в форме фасолины имеет изолированную точку в начале координат $r=0;$
• из точек перегиба присутствуют все две точки

$\cos \varphi =-{\frac {17}{18}},\,$ $r={\frac {10}{9}}a;$

• из вершин попадают на улитку в форме фасолины все четыре точки

$\left[{\begin{array}{lcl}\varphi =0,\,r=5a\,\,{\mbox{и}}\,\,\varphi =\pi ,\,r=a,\\\displaystyle \cos \varphi =-{\frac {2}{3}},\,r={\frac {5}{3}}a.\end{array}}\right.$

Перечислим примечательные точки представителя улитки с параболической точкой распрямления с $l=3a$ (см. рисунок ниже):

• улитка с параболической точкой распрямления имеет изолированную точку в начале координат $r=0;$
• две точки перегиба сливаются в одну параболическую точку распрямления (слияние и исчезновение точек перегиба и вершин типично для кривых, при слиянии «качество» точки меняется в более «сильную» сторону)

$\cos \varphi =-1,\,$ $r=2a;$

• из вершин попадают на улитку с параболической точкой распрямления все четыре точки, но одна попадает на параболическую точку распрямления

$\left[{\begin{array}{lcl}\varphi =0,\,r=6a\,\,{\mbox{и}}\,\,\varphi =\pi ,\,r=2a,\\\displaystyle \cos \varphi =-{\frac {1}{2}},\,r=3a.\end{array}}\right.$

Перечислим примечательные точки представителя выпуклой улитки с $l=5a$ (см. рисунок ниже):

• выпуклая улитка имеет изолированную точку в начале координат $r=0;$
• радиальные координаты кандидатов в точки перегиба

$\cos \varphi =-{\frac {11}{10}}<-1,\,$ $r={\frac {42}{15}}a,$

поэтому точек перегиба нет;

• из вершин попадают на выпуклую улитку все четыре точки

$\left[{\begin{array}{lcl}\varphi =0,\,r=7a\,\,{\mbox{и}}\,\,\varphi =\pi ,\,r=3a,\\\displaystyle \cos \varphi =-{\frac {2}{5}},\,r={\frac {21}{5}}a.\end{array}}\right.$

• Формы эллиптической улитки Паскаля
• 
  Улитка в форме фасолины $r(\varphi )=a(2\cos \varphi +3),\,$ $a=2$ с изолированной точкой, двумя точками перегиба и четырьмя вершинами
• 
  Улитка с параболической точкой распрямления $r(\varphi )=2a(\cos \varphi +2),\,$ $a=2$ с изолированной точкой, параболической точкой распрямления и тремя вершинами
• 
  Выпуклая улитка $r(\varphi )=a(2\cos \varphi +5),\,$ $a=2$ с изолированной точкой и четырьмя вершинами

Уравнения

Уравнение в прямоугольных координатах:

$(x^{2}+y^{2}+ay)^{2}=\ell ^{2}(x^{2}+y^{2}),$

в полярных координатах:

$\rho =\ell -a\sin \varphi ,$

параметрическое:

$x=2R\cdot \cos(t)-h\cdot \cos(2t),$

$y=2R\cdot \sin(t)-h\cdot \sin(2t).$

Здесь a — диаметр исходной окружности, а $\ell$ — расстояние, на которое смещается точка вдоль радиус-вектора (см. конхоида).

При этом начало координат является

• узловой точкой при $a>\ell$,
• точкой возврата при $a=\ell$ (в этом случае улитка Паскаля называется кардиоидой),
• двойной точкой при $a<\ell$.

В случае $\ell =a/2$ улитка Паскаля также называется трисектри́са. Такое название она получила из-за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки. Уравнение трисектрисы:

$z=b(e^{it}+e^{2it})=be^{\frac {3it}{2}}\left(e^{\frac {it}{2}}+e^{\frac {-it}{2}}\right)=2be^{\frac {3it}{2}}\cos {\frac {t}{2}},$

в полярных координатах:

$r=2b\cos {\frac {\theta }{3}}.$

Свойства

Анимация подеры окружности

Построение улитки Паскаля

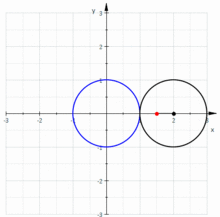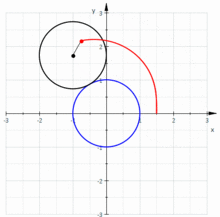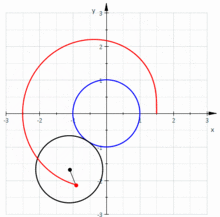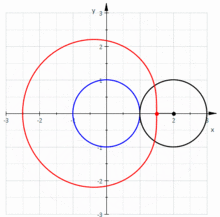
• Улитка Паскаля является подерой окружности относительно любой точки, кроме центра окружности.
• Улитка Паскаля является частным случаем Декартова овала.
• Улитка Паскаля является частным случаем эпитрохоиды.
• Улитка Паскаля является примером эквихордной кривой.
• Длина дуги выражается эллиптическим интегралом 2-го рода.
• Площадь, ограниченная улиткой Паскаля:

  $S={\frac {\pi a^{2}}{2}}+\pi \ell ^{2}.$

При $a>\ell$ площадь внутренней петли при вычислении по этой формуле считается дважды.

Источники

• Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию особенностей: Пер. с англ. И. Г. Щербак под ред. В. И. Арнольда. М.: Мир, 1988. 262 с, ил. (Современная математика. Вводные курсы) ISBN 5-03-001194-3. [J. William Bruce, Peter G. Giblin. Curves and Singularities. A geometrical introduction to singularity theory. Cambridge: Cambridge University Press, 1984.]
• Линия // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1973. Т. 14. Куна — Ломами. 1973. 624 с. с илл., 32 л. илл., 6 л. карт. С. 466—470.
• Паскаля улитка // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 452.
• Савелов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство) / Под ред. А. П. Нордена. М.: Физматлит, 1960. 293 с., ил.
• Соколов Д. Д. Паскаля улитка // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская Энциклопедия», 1984. 1216 стб., ил. Стб. 226—227.
• Улитка Паскаля // Энциклопедический словарь / Гл. ред. Б. А. Введенский, т. 3 Пращур—Яя. М.: «Большая Советская энциклопедия», 1955. 744 с., ил. С. 472—473.
• Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве. Справочник с приложенипем дискеты «Плоские кривые». М.: ФАЗИС, 1997. 334 с., ил. ISBN 5-7036-0027-8.
• Albrecht Dürer Underweysung der Messung, 1525.
• Ferréol Robert. Conchoid // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 6 марта 2023 на Wayback Machine
• Ferréol Robert. Limaçon (or snail) of Pascal // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 12 января 2024 на Wayback Machine
• Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica. Third Edition by Elsa Abbena and Simon Salamon. Studies in Advanced Mathematics: Chapman and Hall/CRC, 2006. 982 p.
• Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
• jan wassenaar limaçon // mathematical curves Архивная копия от 23 июля 2023 на Wayback Machine
• Weisstein Eric W. Limaçon // Wolfram MathWorld Архивная копия от 6 ноября 2020 на Wayback Machine
• Zwikker C. The Advanced Geometry of Plane Curves and Their ApplicationsThe Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 10: 0486610780. ISBN 13: 9780486610788.

Литература

• Limacon of Pascal at The MacTutor History of Mathematics
• Limacon of Pascal at Visual Dictionary of Special Plane Curves
• A red limaçon of Pascal - построение в Sage Math с использованием библиотеки Matplotlib